1. Ad hoc uncertainty factors
2. Classical probability theory (Bayes Theorem)
3. Fuzzy set theory
4. Dempster Schaffer theory evidence

1. Relevant domain is random
2. Relevant domain is not random, rarely have access to enough data
3. Domain is not random, just not described in sufficient detail

1. How are certainties associated with antecedents?
2. How a rule translates input certainty to output certainty?
3. How do you combine fact certainty with several rules argue support?

Certainty Factors (ad-hoc)

how certain are you that the rule will fire?

• (0.9)(1.0) = .9
• (0.25)(1.0) = .25

P(E) = Number of desired outcomes / Total number of outcomes = | event | / |sample space|

P(not E) = 1 – P(E)

P(A or B) = P(A) + P(B) – P(A Ç B) P(A Ç B) = f ( a and b are mutually exclusive)

P(A Ç B) = P(A) * P(B|A) = P(B) * P(A|B)

For independent events

P(B|A) = P(B)

P(A|B) = P(A)

P(H_i |E) º Probability H_i is true given evidence E

P(E | H_i) º Probability evidence E is observed given H_i is true.

P(H_i) = H_i true regardless of evidence

P(H_i |E) = P(E | H_i) * P(H_i) / S P(E | H_k) * P(H_k)

Tanimoto Example on Rain in Seattle

• Prior Probability it will rain

• Geese on the lake, given rain tomorrow

• Geese on lake, with no rain tomorrow

Probability of rain tomorrow with geese on the lake

P(H | E) = (P( E | H) * P(H)) / P(E) = (0.016 / 0.021) = 0.7619

P(E) = P(E | H) * P(H) + P(E | ~H) +P(~H) = (0.02)(0.8) + (0.025)*(0.2) = (0.016) + (0.005) = 0.021

P(~H | E) = ?

P( ~H | E) = (P(E | ~H)P(~H)) / P(E) = (0.005 / 0.021) = 0.2381

1. Difficult to get all apriori and joint probability required
2. Database of priorities is hard to modify because of interactions
3. Lots of calculations
4. Outcomes must be disjoint
5. Accuracy depends on complete hypothesis

1. Information available is of varying certainty or completeness
2. Need nearly optimal solutions
3. Need to justify decisions in favor of alternate decisions
4. General rules of inference are known or can be found for the problem

X Î S This is not longer true

X Ï S Either in or out for most set theory

Question?

What constitutes a big pile of chalk?

If we have three pieces of chalk in the room is that considered a big pile of chalk? Some people might say, yes that is a big pile and some would not. Someplace between those three pieces of chalk and a whole room full of chalk the pile of chalk turns from a small pile into a big pile. This could be a different spot for different people.

F:[0,1]ⁿ ® [0,1]

{0,1}

Tanimoto has examples of independent events and dependent events

P (X ® (X n Z))

P(X) = 0.5 Possibilistic

P(X) = 0.1 P(Y n Z) = max (P(Y),P(Z))

P(Z) = 0.2 P(Y n Z) = max(0.1, 0.2) = 0.2

P(X ® P(Y n Z)) = max(1-P(X), P(Y n Z))

= max(1-(5), 0.2)

= 5

Probabilistic

P(Y n Z) = P(Y) + P(Z) – P(Y)P(2) = (0.1 + 0.2) – ((0.1)(0.2)) = (0.3 – 0.2) = 0.28

P(X ® X n Z) = 1 – P(X) + P(X)P(Y n Z) = (1 – 0.5) + ((0.5)(0.28)) = 0.5 + 0.14 = 64

• Tanimoto pg. 342, pg. 338 car starting

S1: Clanking Sound

S2: Low pickup

S3: Starting problem

S4: Parts are hard to find

C1: Repair Estimate > $250

H1: Thrown connecting rod

H2: Wrist Pin Loose

H3: Car Out of Tune

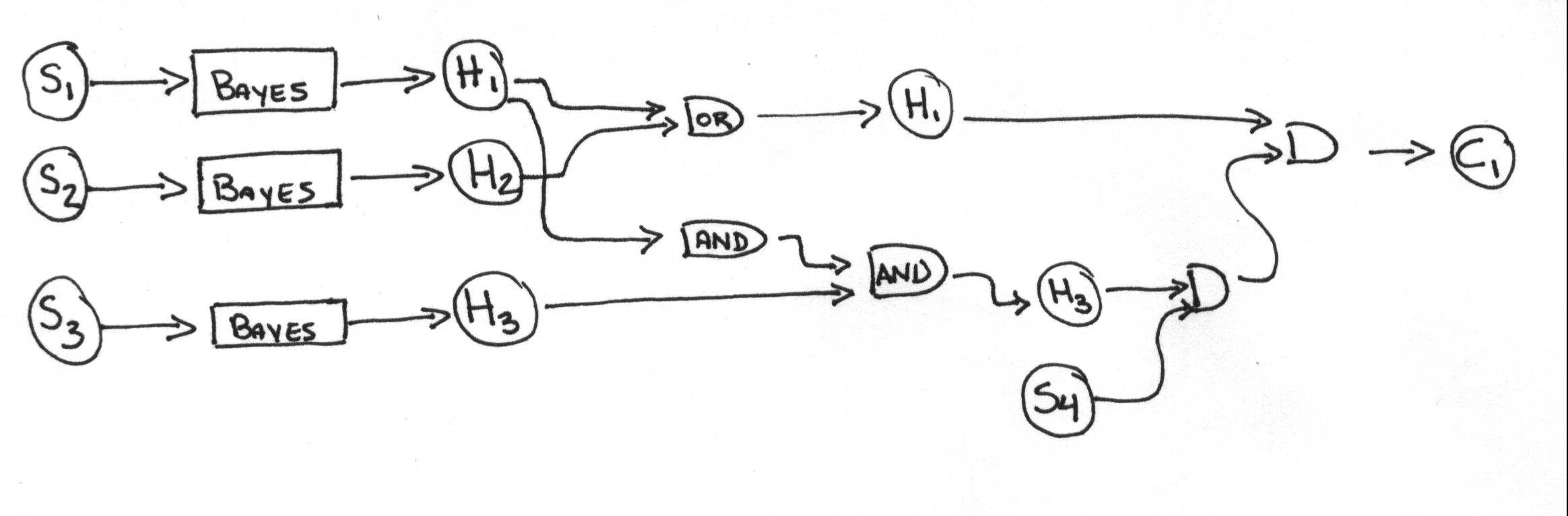P(H: | S)

Second Level

H4: Replace or Rebuild Engine

H5: Tune Engine

1. Determine relevant inputs
2. Determine states of decision alternatives
3. Determine intermediate assertions
4. Formulate inference links

1. Logical Occurrence (+ Correlation)
2. Negative Occurrence ( - Correlation)
3. Logical Implication
4. Conjunction (and)
5. Disjunction ( or )
6. Exclusive Disjunctive (XOR)
7. Fiddle with probabilistic of inferences

X,Y,Z

{ X } { Y } { Z }

{ X,Y } { X,Z } { Y,Z } ® [0,1]

{ X,Y,Z } { }

This all needs to add up to 1

as more evidence is acquired views might change

Belief

B(A) + B(~A) ¹ 1

A = total exposed spots is 7

6 of 36 elements from m

m Î P(m ) ® [0,1]

m(f ) = 0

S m (x) = 1

m ³ A

m ³ F

Evidence

m(F) = 1 ® Evidence is certain

F Ç A ¹ 0

Belief (A) = S m(B), A ³ B

Doubt in (A) = Belief (> A)

Plausibility (A) = 1- Doubt(A)

Belief (f ) = 0 Plausibility(f ) = 0

Belief(m ) = 1 Plausibility(m ) = 1

Plausibility (A) ³ Belief (A)

1 ³ Belief(A) + Belief(~A)

Plausibility(A) + Plausibility (~A) ³ 1

If B ³ A then

Belief (B) ³ Belief A

Plausibility (B) ³ Plausibility (A)

Rule of combination for uncertainty evidence – Orthogonal

A ¹ f

if true

[m1 + m2] A = S _{xny = A} M1(x)M2(y)

1 - S _{xny = f} M1(x)M2(y)

if A ¹ f then [M1 + M2] f = 0

Numeric Example

S = Snow

R = Rain

D = Dry

m = {S, R, D}

|P(m )| = 8

p. 275 Tanimoto

Two Pieces of evidence

1. Temperature is below freezing (temp < 32 degrees F or 0 degrees C
2. Barometric Pressure is falling (storm likely)

All values in the chart should add up to one

The belief ({S,R}) = Mboth({S,R}) + Mboth({S}) + Mboth({R}) = 0.744