Knowledge Representation for Artificial Intelligence (CIS 479)

Prolog

logic- predicate logic or propositional logic

P º "the apple is red" [propositional logic example]

red (apple) [predicate logic example]

isa (bear, mammal) [predicate logic example]

Declarative Programming - use depth-first search & pattern matching instead of through conventional programming.

Production Systems

Procedural knowledge

aka "How to knowledge"

Relational Database

Semantic Networks

Perspective

Semantic Networks

Frames

Scripts

Conceptual Dependency

Types of Knowledge

  1. objects – physical & concepts
  2. Events- maybe time, maybe cause & effect
  3. Performance (how to)
  4. META Knowledge – knowledge about how to use knowledge

Stages of knowledge use

  1. Acquisition
  2. Retrieval (recall)
  3. Reasoning

Knowledge Representation Issues

  1. Grain Size – Resolution Detail
  2. Scope
  3. Modularity
  4. Understandability
  5. Explicit Vs. Implicit Knowledge
  6. Procedural Vs. Declarative knowledge

Advantage of Procedural Knowledge
  1. Store each fact once
  2. Easy to add new facts

Advantage of Procedural Knowledge
  1. Easy to Represent "how to"
  2. Easy to represent any knowledge not fitting declarative format
  3. Relatively easy to implement heuristic stuff

Good Knowledge Representation Scheme
  1. Represential Adequacy – all knowledge in problem domain
  2. Inferential Adequacy – ability to manipulate structures to desire new structures
  3. Inferential Adequacy – Incorporate new knowledge & focus attention
  4. Acquisition – Easy to add facts
  5. Semantic Power
    1. Support Truth theory
    2. Constraint Satisfaction
    3. Cope with incomplete or uncertain knowledge
    4. Some Common Sense Reasoning Capability

Knowledge Representation
  1. Properties in every domain? - if so what are they...
  2. At what level should knowledge be represented?
  3. Given a large amount of knowledge, how do you access the relevant parts quickly

® = is a

¬ = a kind of

dog ® pet ® living think

® = is part of

¬ = has a part

finger ® hand ® body

Knowledge Representation Problems

  1. Initial selection at best structure
  2. Fill in details from current situation
  3. Find better structure if first choice is bad
  4. None of available structures are appropriate
  5. When to create and remember a new structure

Slot & Filler

(putprop ‘dog ‘animal ‘isa)

(putprop ‘animal ‘dog ‘ako)

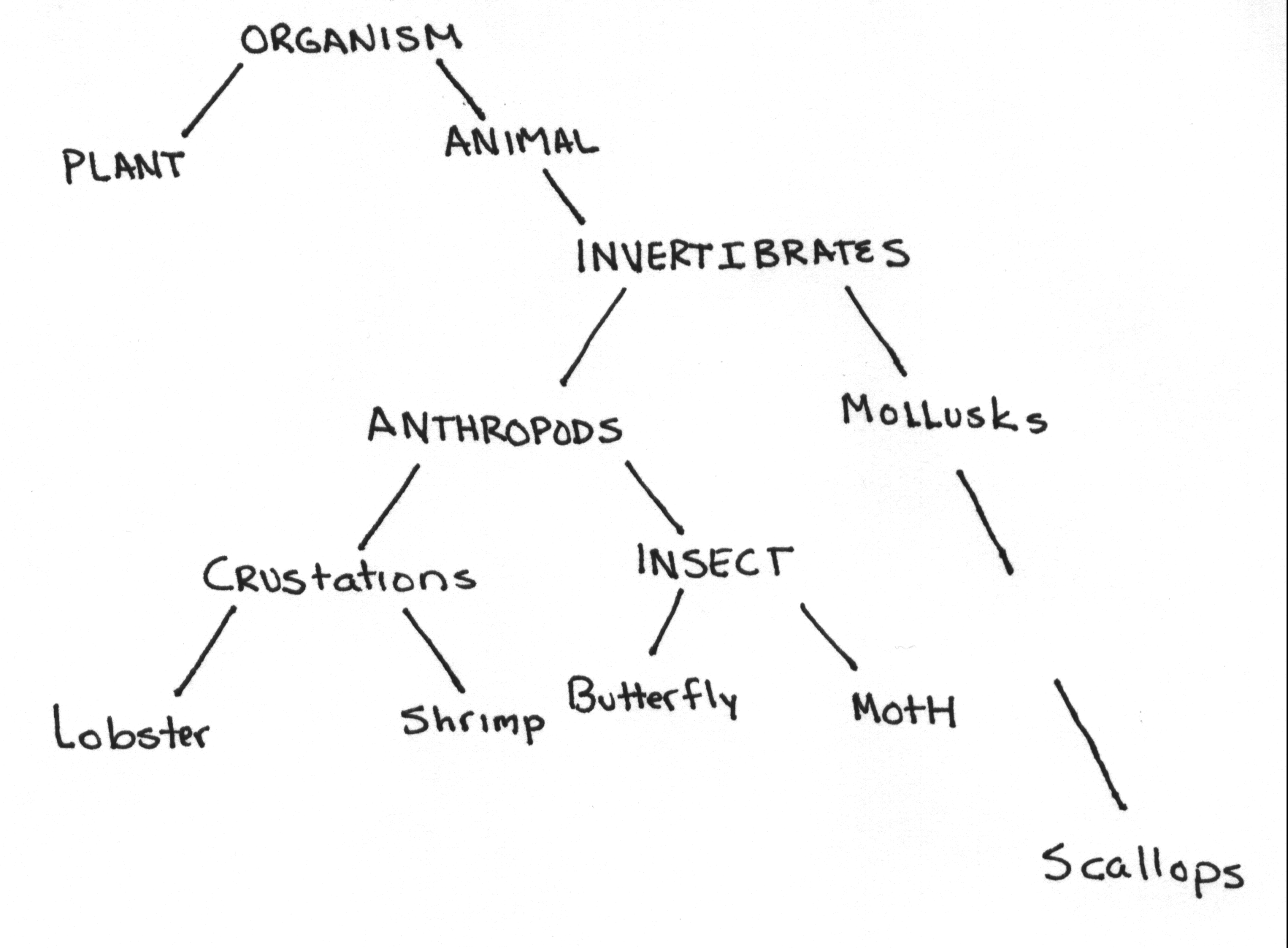
x = lobster
y = animal
n = scallop

(defun isatest ( x y n) (cond ((EQ x y) 7)

(( ? group n) nil) ((member y(get x ‘isa)) y) (t (ary mapcar #’lambda (xx) (isatest x x y) (1 – n)) (get x ‘isa)) ) ) (defun any (l) (cond ((null l) nil) ((car l) t) (T (any (cdr l)) ) )

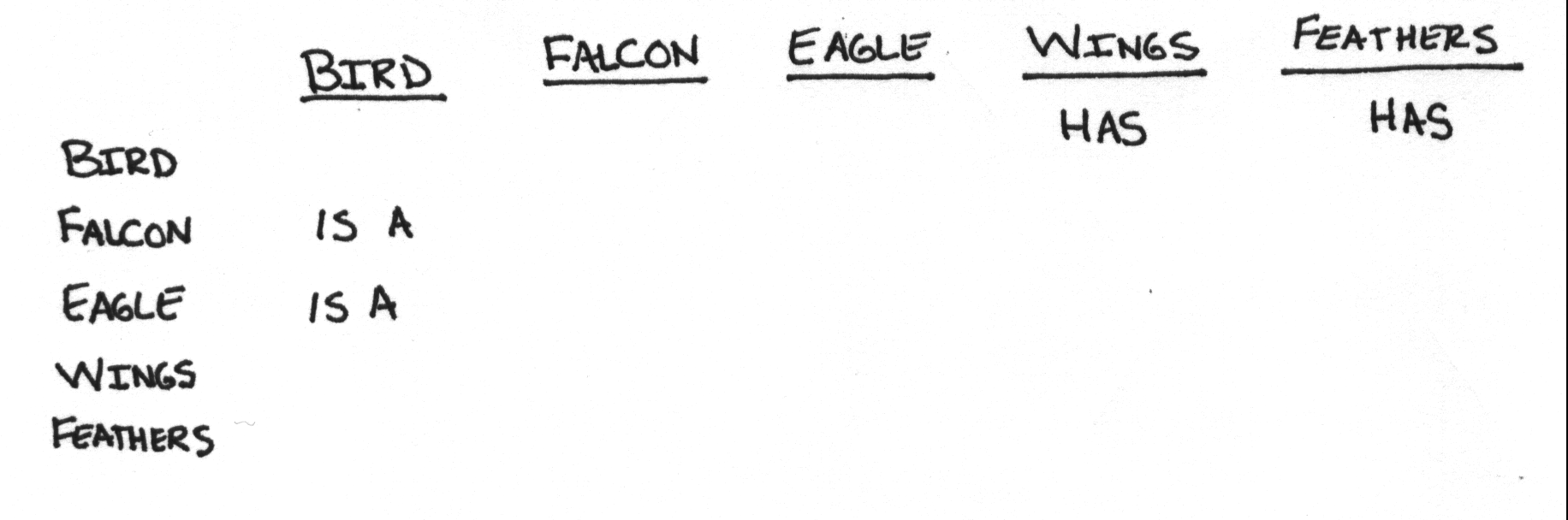
Relationship Matrix

Value Inheritance Procedure

[f = node, s = slot / property]

  1. Form a queue consisting of node f and all class nodes found in f’s isa state
  2. Until queue is empty or value found if queue front has value in s then value found else remove first queue element and add nodes related by isa
  3. If value found then repeat it else announce fail.

If Needed Inheritance

[f = node, s = slot / property]

  1. Form a queue consisting of node f and all class nodes found in f’s isa state
  2. Until queue is empty or value found if queue front has procedure to compute S value then value found else remove first queue element and add nodes related by isa
  3. If value found then repeat it else announce fail.

Default Inheritance

[f = node, s = slot / property]

  1. Form a queue consisting of node f and all class nodes found in f’s isa state
  2. Until queue is empty or value found if queue front has default value in s then value found else remove first queue element and add nodes related by isa
  3. If value found then repeat it else announce fail.

N-Inheritance

This method uses all three inheritance methods previously mentioned "veritcally". First uses "value" leaf to root, then "if-needed" leaf to root, and lastly "default" leaf to root.

Z-Inheritance

Uses all three inheritance type "horizontally" - at each level tries "value", "if-needed", and "default".

Frame- preprinted semantic network

Infer unobserved attributes

  1. Frame contains information that can be used even if not observed
  2. Frame contain attributes true of all instances
  3. Frames contain typical instances of the object

What happens if "fleshing out" fails?

  1. Select fragments of current situation that match and match against other frame candidate.
  2. Make excuse for failure and use frame anyway.
  3. Refer to list of stored links.

  4. Inheritance links

dog ® mammal ® animal(living things)

Weakness of Frames

  1. Tend to not be frame like
  2. Definitions are important
  3. Cancellation of default properties is tricky

Scripts

Script attributes

  1. Entry condition
  2. Result
  3. Props
  4. Rules
  5. Tracks
  6. Scenes

Strengths

  1. Scripts can predict events and answer questions
  2. Provide a framework for integrating observations into coherent interpretation
  3. Provide means for detecting unusual events

Criticisms

  1. Ad hoc
  2. Either scripts only account for details in a restricted domain so they are not interesting or they apply everywhere which is not likely.

Relational Database

Relations ® tables

first second third

object relation object

if X? isa horse
   X? is-parent-of Y?
   Y? is fast

then X? is valuable
  1. Select data with second equal to isa and third equal to horse {creates temp set}
  2. Project result will be first and call it A1 {horses}
  3. Select data with second equal to is parent
  4. Project result over? first and third and call it A2 {gives parent child}
  5. Select data with second is and third equal fast
  6. Project result over first
  7. Join A1 and A2 with A1 first equal A2 first {horses with children}
  8. Join B1 with A3 with B1 third A3 first.
  9. Project result with first

For A Data Sets

For B Data Sets

with m rules