• Babbage wanted to create a program to solve a chess game
• Good Domain

1. Provided a structured task with clear success
2. Games did not require much knowledge

• Chess average branch is 35^100th

1. improve generator (generator only generates the best move)
2. improve tester ( so bad moves are known immediately)

• How do you know what move leads to win/lose? (This is a problem)

1. complete
2. non-redundant
3. informed

Depth + 1

1 move

2 moves

Minsky’s credit assignment problem? This is when you try to decide what move actually caused the win or lose in the game.

Turing (chess) white/black

Samuel’s (checkers)

Linear combinations C1 * piece advantage
+ C2 * center control
+ C3 * advantage center
+ some other things

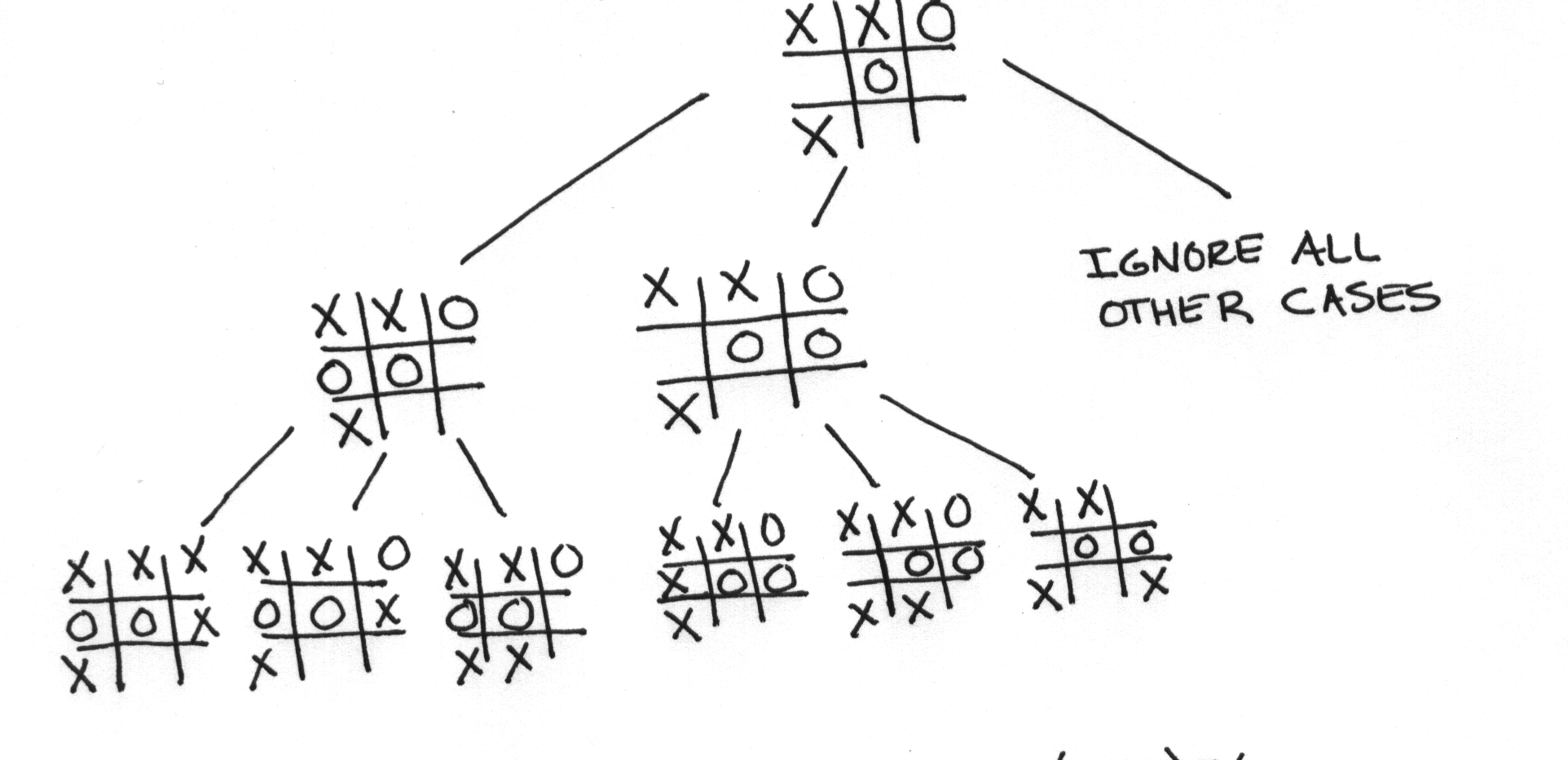
Tic Tac Toe

100A + 10B + C – (100D + 10E + F)

A = number of lines with 3 X’s
B = number of lines with 2 X’s
C = number of lines with single X
D = number of lines with 3 O’s
E = number of lines with 2 O’s
F = number of lines with a single O

How do you know when the search criteria has been reached?

1. Somebody won
2. Number of ply
3. Promising path
4. Time left
5. Stability of position

• You don’t have to look at all the arguments!

     max = -3            A
                      /     \
     min = -6       B         C      min = -3
                  /   \     /   \
                 D     E   F     G 
    static       9    -6  -4    -3
    evaluation 

Function Mini-Max(current position)
begin
  if (limit of search is reached) then
    begin
      compute static value of current position
      report result
    end
  else if (level is minimizing) thee
    begin
      use mini-max on the children of the current position
      report minimum of the results
    end
  else
    begin
      use mini-max on the children of the current position
      report maximum of the results
    end
end

• This will out perform mini-max twice as much will be done at a time
• Aplha cut-off : this will occur whenever a min. node descendant receives a value less than the alpha known to the main nodes parent, which will be a max node. The final value, min. value can be set to Beta.
• Beta cut-off: whenever a max node descendant receives a value greater than Beta known to the max nodes parent, the final value of max node can be set to alpha

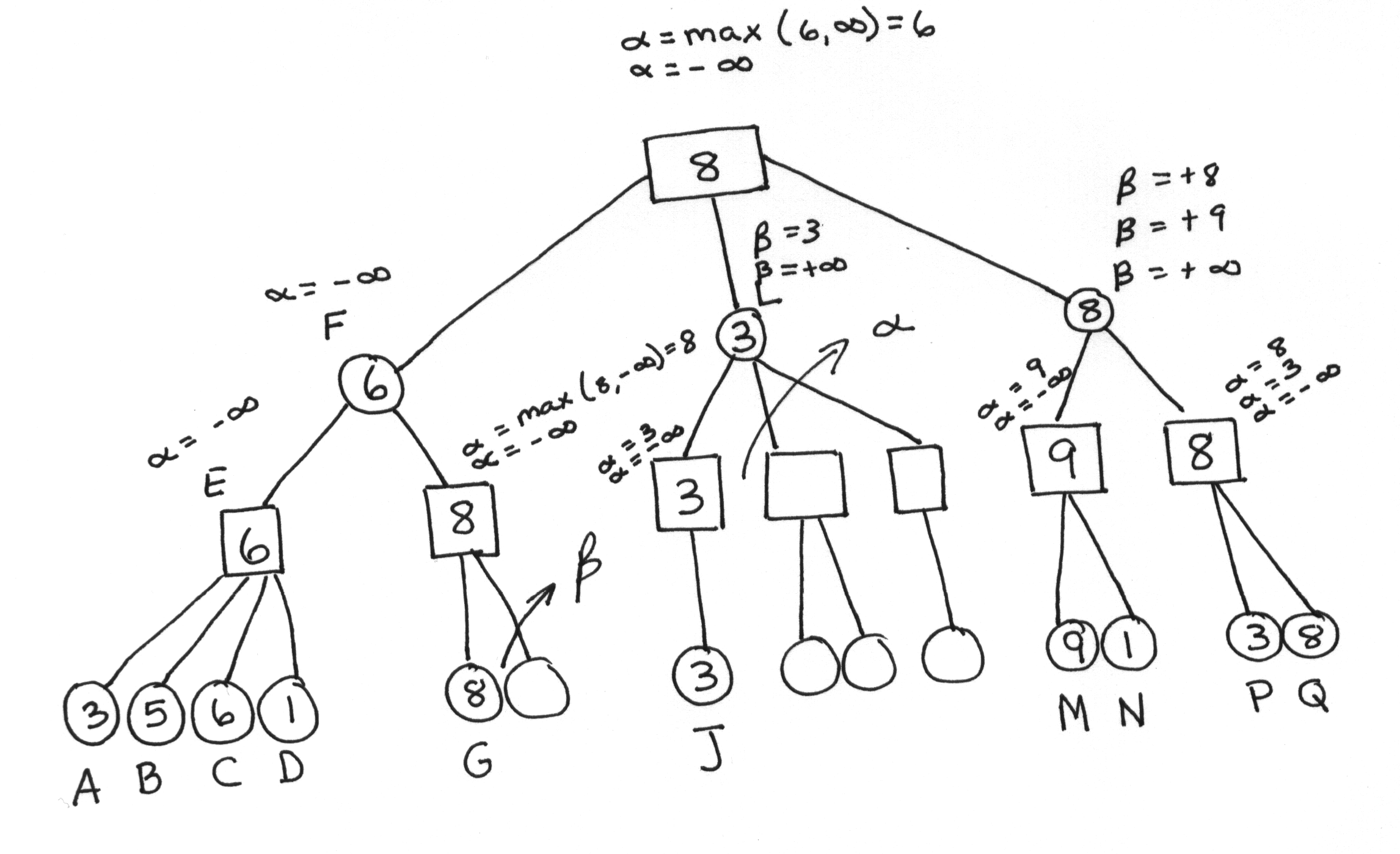
A a = max ( - infinity, 3 ) = 3

B a = max ( 5, 5) = 5

C a = max (3, 6) = 6

D a = max ( ) = 1

Some C ++ code for the min-max algorithm

Umdsun1.umd.umich.edu/CIS/course.des/cis479/testab.cpp

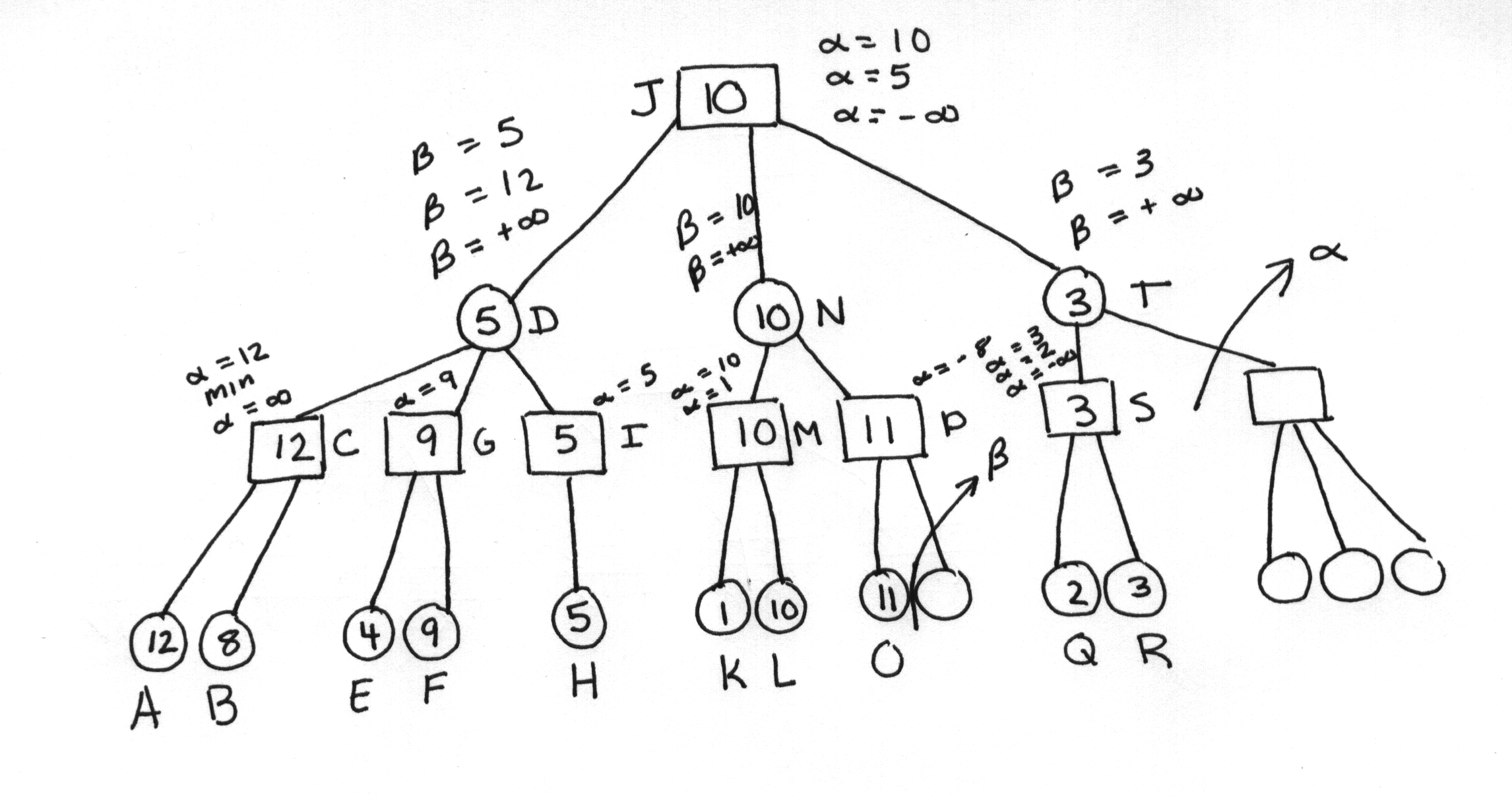This cuts off at the fourth static evaluation!

Alpha/Beta Function

Function Value (P, µ , b ) // P is the position in the data structure
begin
// determine successors of P and call them
// P(1), P(2), ... P(d)
  if d=0 then
    value f(p) // static evaluation function
  else
    begin
      m = µ 

      for i =1 to d do
        begin
          t = - value (Pi - b , - m)

          if t > m then
            m = t

          if => b then
            exit loop
        end

      value = m
    end
end

Alpha/Beta

we examine n nodes at depth D (without alpha / beta pruning) we can examine n nodes at depth 2*D

mini-max with µ /b Pruning

• Win/loss could be the next move and it is hard to say what it will be. IF you stop at a three ply search, you don’t know if the next level will cause a win or loss for you.

Progressive Deepening- with this process the increase in cost is not to great. If you have extra time you could expand the tree a little bit farther until you run out of time.

Heuristic Pruning- This is where you throw out the moves that are no good or the moves that make no sense. Branch rules could be used to take care of this.

Heuristic Continuation- This will continue a path to see what could happen if you take a certain path through the tree.

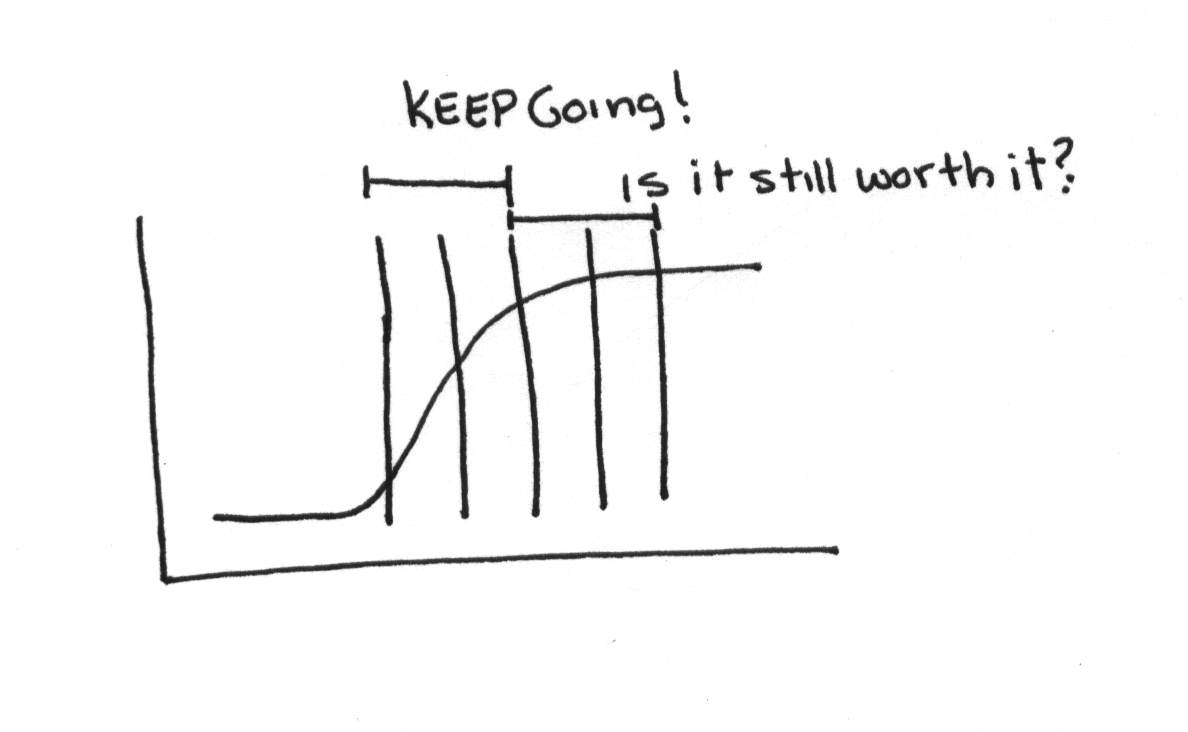
Futility Cutoff- This is where you decide if it is worth continuing as the growth rate decreases.

Secondary Search

• pick a level
• alpha / beta pruning or mini-max search

Book Moves- This is where you use moves that have already been proven to work.

• Search is a weak AI method, you should use search only when you don’t have enough knowledge.