CIS 400 LECTURE 6

BNF

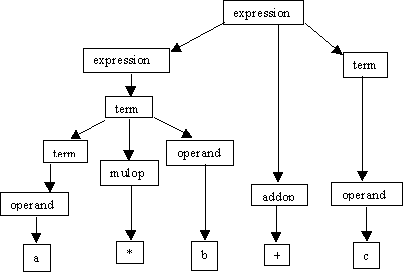
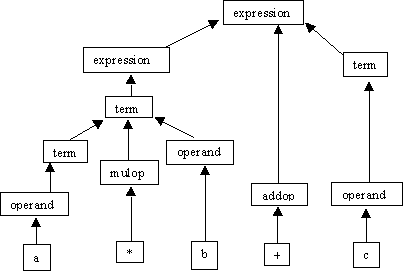
Expression ::= term | expression addop term

Term ::= operand | term mulop operand

Operand ::= a | b | c

Addop ::= + | -

Mulop ::= * | /

Natural ::= digit

Integer ::= [ +|- ] natural

Digit ::= 0 | 1 | 2 | 3 | 4 | …

Top down parsing: a*b+c

Bottom up parsing:

Syntax graphs:

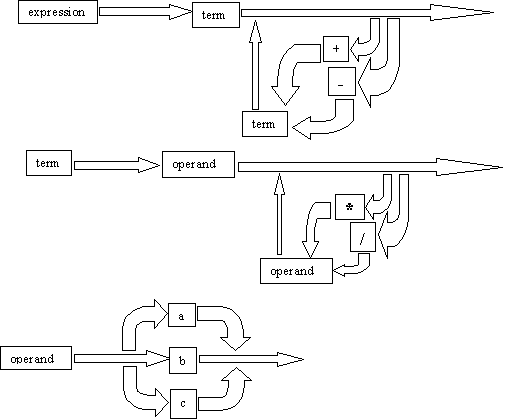
CBL, (Cobol-Like-Grammar)

· Optional element []

· Alternatives <>

· Optional alternatives

· repeated elements …

· underline or boldface key words or reserved words

Parser:

Series of sub-routine calls:

Nested "if/then else", (with error trap)

"while" (conditions) "do"

if (symbol a) = terminal

read next char

else

error

Semantics:

· operational semantics

· formal semantics

v axiomatic semantics

v denotational semantics

v attribute grammars

Formal semantics, (why?)

· rigorous and unambiguous definition

· provides a basis for language comparison

· implementation independent

· basis for correctness group of language implementation

· basis for program proofs

Axiomatic semantics, (chapter 3, page 134)

· predicate calculus

· logical expression involving program variables used to describe state of computation

EXAMPLE: for assignment statement

Pre-condition à {x = x₀ and y = y₀}

z ß x + y

Post-condition à {z = x₀ + y₀}

Default assertion:

If you don't see a value of a variable, either it doesn't exist or doesn't change

à {x = x₀} where x₀ is initial value

if (x < 0) then

{x = x₀ and x₀ < 0}

y = -x

{y = |x₀|}

else {x = x₀ and (x₀ >=0)}

y¬x

{y = |x₀|}

if {( x₀ < 0 and y = -x₀ ) or (x₀ > 0 and y = x₀)}

The above is obviously "absolute value"

®{x = x₀, z = z₀, y >= 0}

while y<> 0 do

{x = x₀, z = z₀}

z ¬z + x

{z = x₀ + z₀}

{y = y₀}

y ¬ y - 1

{y = y⁰ - 1}

end while

{ y = 0, z = z₀ + y₀ * x₀ }

Loop invariant

Execution continues

while (y >=0 and z = z₀ + y₀ * x₀) where y₀Î natural numbers