CIS 400 LECTURE 5
Syntax
·
Defined
as set of rules specifying legitimate sequence of characters for allowable
programs
·
Grammar
º set of rules
Semantics
·
Meaning
assigned to syntactic constructs
Characteristics
of good syntax
·
Readability
·
Writeability
·
Redundancy
·
Easy
to translate
·
Lack
of ambiguity
Program
structure and sub-structure
·
Separate
sub-program definitions
·
Nested
sub-programs
·
Separate
data from code (i.e. pre-compiled headers in C++)
·
Un-separated
sub-programs
Language
grammar
"T"
is some alphabet for some set of languages
{character
set for machine}
T*
all possible sequences: "strings", "words" or
"tokens"
"language"
is some sub-set of T*
Language
is a 4-tuple
L(T,
N, P, S) T = terminal N = non-terminal P = productions S =
start
Generative
grammars
Let
a,b Î T
A,B,S Î N
P: S®aAB rule 1 S is start
S®a rule 2
A®bs rule 3
B®b rule 4
Derivation
example
S ® aAB by rule 1
aAB ® abSB by rule 3
abSB
® abSb
by rule 4
abSb
® abab
by rule 2 (this is considered
a "derivation")
Finite
state machine
·
Finite
number of states (N: non-terminals)
·
Start
state (S: where S Î N)
·
Final
states (FÍ N)
·
Sets of inputs (T or alphabet)
·
Transition function: dI =T C N® N
T = {a,b} F = {S2} N = {S0, S1, S2,
S3}
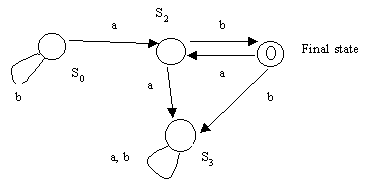
|
|
a |
b |
|
S0 |
S1 |
S |
|
S1 |
S3 |
S2 |
|
S2 |
S1 |
S3 |
|
S3 |
S3 |
S3 |
For derivation aabbaabbab: state is "stuck" in S3
For derivation bbbabab: arrives in final state S2
bn(ab)(ab)m is accepted by this machine, (also represented as b*(ab)+
expression)
Four classes of grammars (per Chomsky)
·
Regular, (where x & y are null): at most one non-terminal
A®a
Þ S®e (allowed only
if NOT A®S)
A®aB
·
Context-free grammars, (x & y are null), ZÎ(T È N)*
A®e
A®abAbB
·
Context-sensitive, ( xAy®Z, where x,y,z Î (N È T)*)
S®e (if S never on RHS)
AaBS®abbBBa
·
Unrestricted, (a.k.a. recursively enumerable): no restrictions
Regular expression accepted by finite state machine
CFG accepted by push-down automata
·
Current state
·
Top of stack symbol
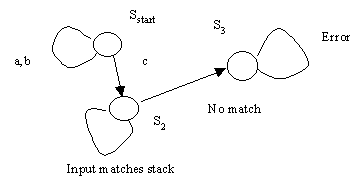
Procedure for this push-down automata
Add a,b,c to stack. If a or b, remain in S. Else if c, move to S2. Once in S2, pop
the stack, then:
1) if input matches stack, erase input symbol
2) if no match, go to S3
3) if input ends and stack not empty, go to S3
Context-sensitive grammar accepted by a "linear bound
automaton", (similar to a Turing machine but with a finite input tape).
Unrestricted grammar accepted by a Turing machine
·
infinite input tape
·
read/ write head
·
finite instruction set
Turing machine represented by a 5-tuple, T=(S1, a, S2,
b, M)
S1 º current machine
state
a º symbol
"under" the read/ write head
S2 º next state, (in
machine)
b º symbol to
replace, or written over, "a"
M º move instruction,
instructs to move left or right on TAPE
TOP-DOWN PARSING
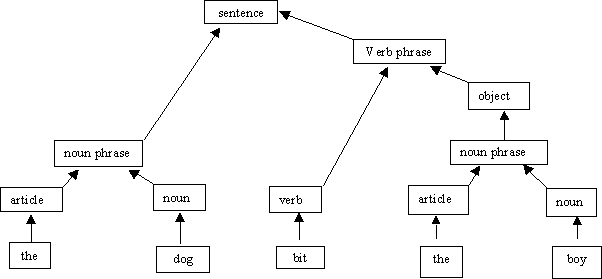
EXAMPLE: the dog bit the boy
Sentence::= noun phrase verb phrase
Noun phrase::= article noun
Verb phrase::= verb object
Object::= noun phrase
Article::= the | a | an
Noun::= dog | boy | girl
Verb::= bit | saw | wrote
Bottom-up parsing